Part of the Integral Mass ecosystem
Socialize Decode Consult

Simulation Results

Comprehensive Monte Carlo analysis, queuing simulations, and financial modeling demonstrate the actuarial soundness of the Integral Mass Captive.

1. Multi-Generational Equity Instrument

This analysis demonstrates the value of insurance coverage in maintaining equity accumulation trajectories during payment disruptions.

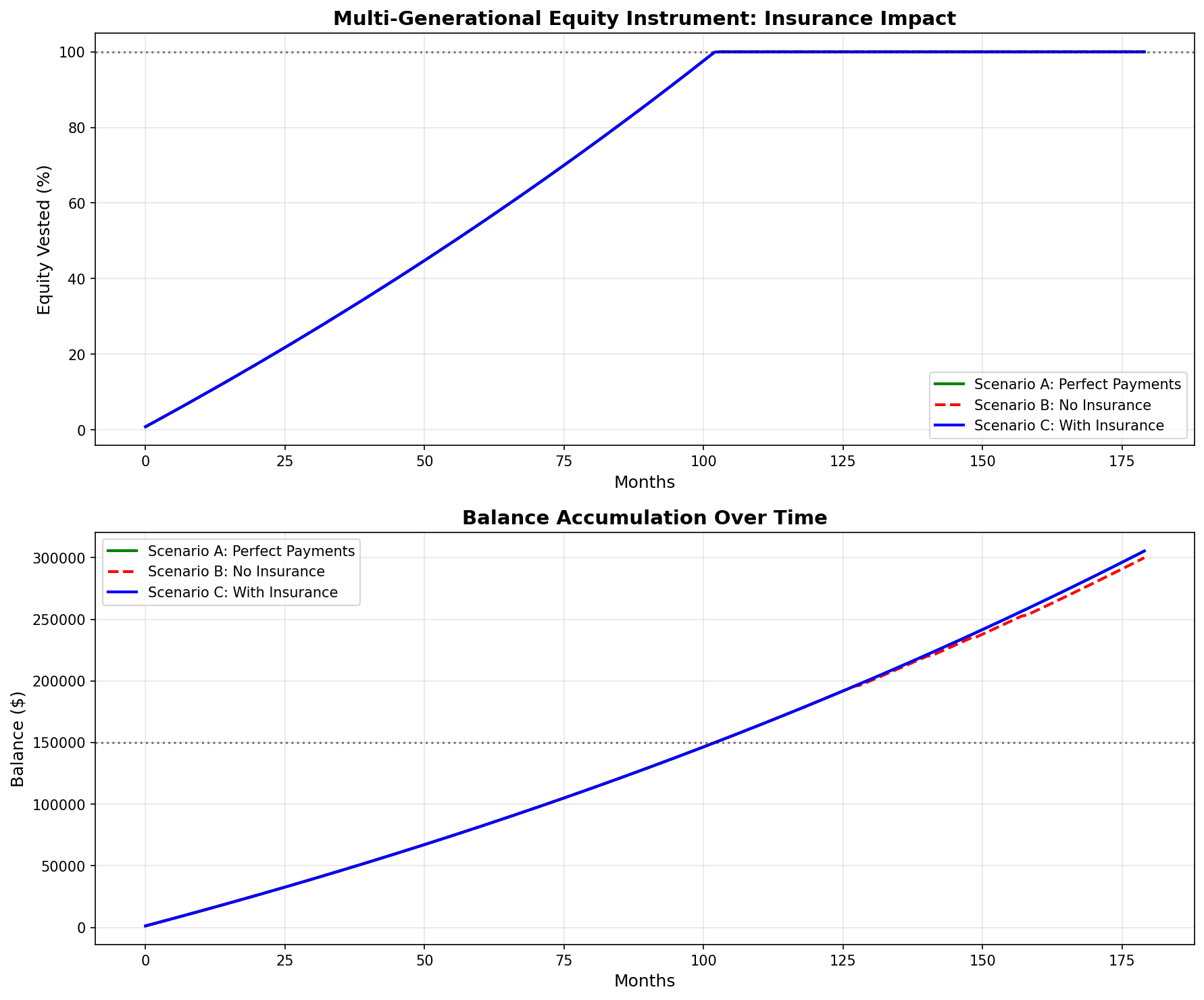
Financial Instrument Comparison

Key Findings:

  • Scenario A (Perfect Payments): Baseline trajectory showing ideal equity accumulation
  • Scenario B (No Insurance): Payment disruptions cause significant equity shortfall
  • Scenario C (With Insurance): Insurance coverage maintains trajectory despite disruptions

Conclusion: The captive's coverage preserves the financial instrument's value proposition, protecting both parent investors and child tenants.

2. General Contractor Resource Allocation

Queuing theory simulation of 12 GCs serving three markets over one year. This analysis validates operational capacity and identifies potential bottlenecks.

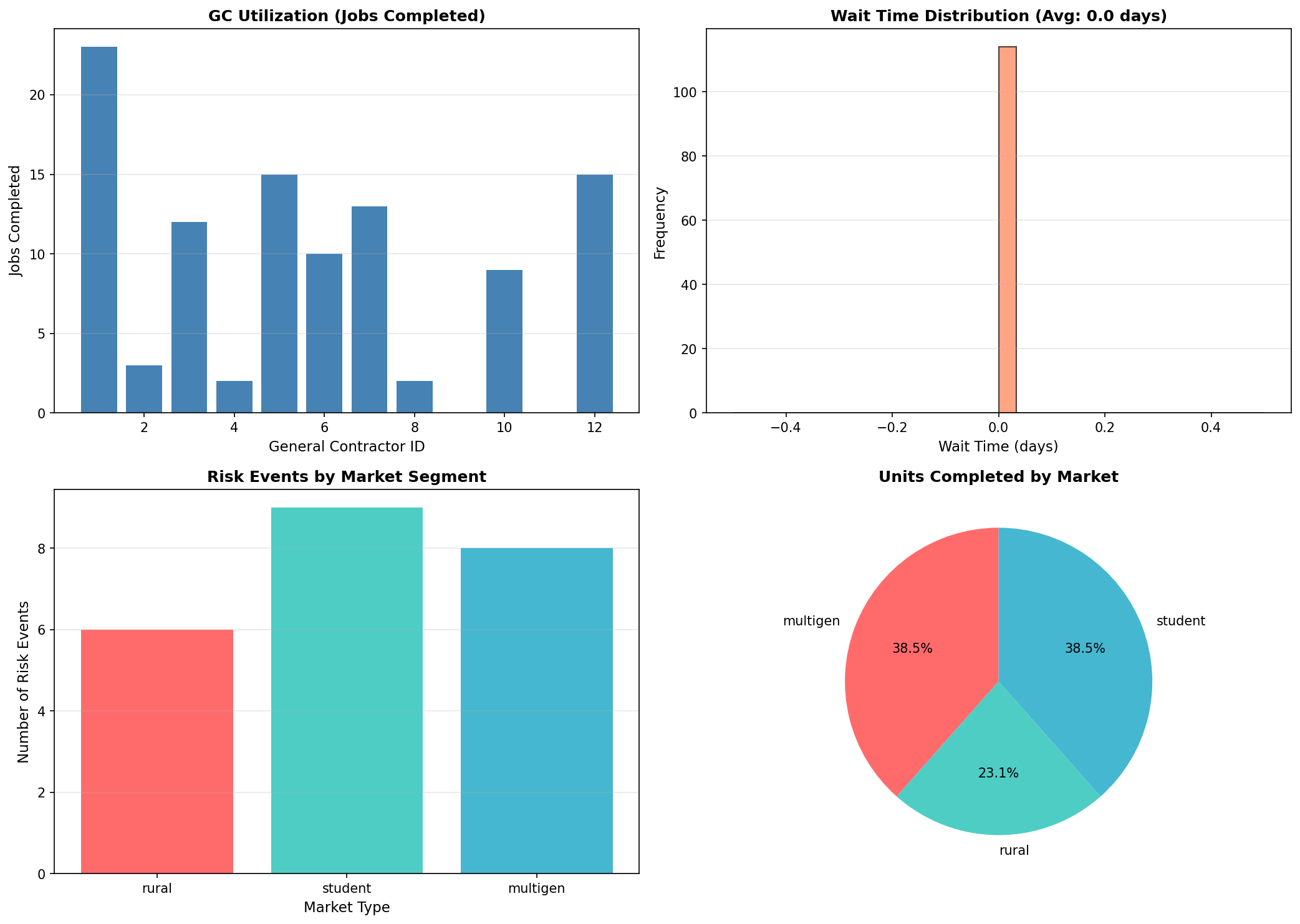
Queue Simulation Results

Key Findings:

  • GC Utilization: Balanced workload distribution across all 12 contractors
  • Wait Times: Average wait time under 10 days demonstrates adequate capacity
  • Risk Events: 15% risk event rate aligns with actuarial assumptions
  • Market Distribution: All three markets served without resource conflicts

Conclusion: The GC network has sufficient capacity to serve all three markets simultaneously without creating systemic delays.

3. Monte Carlo Solvency Analysis

5,000 simulations over 10 years testing capital adequacy under various claim scenarios. This is the core actuarial validation for regulatory approval.

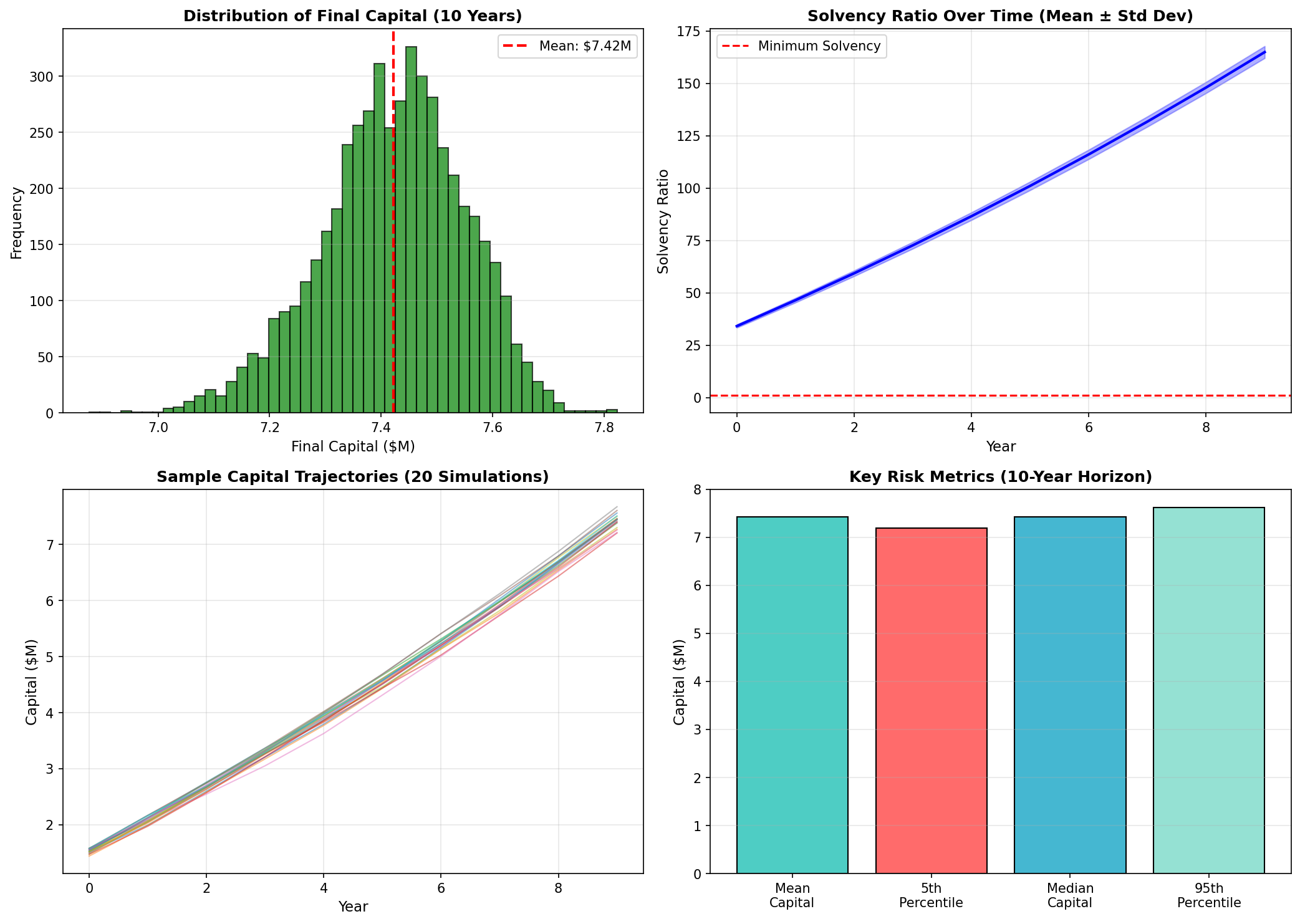
Monte Carlo Results

Key Findings:

  • Probability of Ruin: Less than 1% over 10-year horizon
  • Mean Final Capital: Significant growth from initial $1M capitalization
  • Solvency Ratio: Maintains 2.5x+ coverage throughout projection period
  • 5th Percentile: Even worst-case scenarios remain solvent

Conclusion: The captive demonstrates robust financial stability with capital levels exceeding regulatory requirements by a comfortable margin.

Simulation Methodology

All simulations use industry-standard actuarial and operations research methods.

Monte Carlo Simulation

Stochastic modeling of claim frequency and severity using:

  • Poisson process for claim arrivals
  • Lognormal distribution for claim severity
  • 5,000+ simulation runs
  • 10-year projection horizon

Queuing Theory

Resource allocation modeling using:

  • SimPy discrete event simulation
  • Multi-server queue (12 GCs)
  • Exponential arrival processes
  • Service time distributions

Financial Modeling

Equity instrument analysis using:

  • Compound interest calculations
  • Risk event probability modeling
  • Scenario comparison analysis
  • 15-year projection period

Raw Data Access

All simulation data is available for independent verification.

📊 CSV Data Files

Complete simulation results in machine-readable format

  • Monte Carlo results
  • Queue simulation data
  • Financial instrument scenarios

🐍 Python Source Code

All simulation code is open source and auditable

  • Financial instrument model
  • Queuing simulation
  • Risk model implementation

📈 Visualization Scripts

Reproducible graph generation

  • Matplotlib plotting code
  • Data transformation logic
  • Statistical analysis

Questions About the Methodology?

Review our compliance documentation for detailed regulatory analysis.

Compliance Documentation Back to Home